XYLENE POWER LTD.

GLOBAL WARMING

By Charles Rhodes, P.Eng., Ph.D.

INTRODUCTION:
This web page shows that doubling the atmospheric CO2 concentration from its November 1996 value of 360.76 ppmv causes a temperature increase over dry land of about 2.923 degrees C.
 

WARMING EQUATION:
Recall from the Radiation Physics section at radiant energy balance the Earth's emission temperature Ta seen from space is:
Ta = Te [(1 - Fr) / Ft]^.25
where:
Fr = the albedo at solar wavelengths
Ft = the emissivity at thermal infrared wavelengths
Te = theoretical average temperature defined by:
Te = (Ho dAc / dAs Cb)^.25

Due to the rotation of the earth, which causes alternating solar exposure and darkness, at any location in the Earth's atmosphere there are daily oscillations in the local atmospheric water vapor concentration. However over time these oscillations average out.

At any particular location the average temperature Te is constant as long as the solar irradiance Ho is constant and the earth's shape, axial orientation with respect to the sun and orbital path remain constant. Note that the Earth's axial orientation with respect to the sun oscillates with a period of one year.
 

SENSITIVITY OF Te TO Ho:
The above equation for Te can be rewritten as:
Te^4 = (Ho dAc / dAs Cb)
Differentiating gives:
4 Te^3 dTe = (dAc / dAs Cb) dHo
Divide through by Te^4 to get:
4 dTe / Te = (dAc / dAs Cb) dHo / Te^4
= (dAc / dAs Cb) dHo / (Ho dAc / dAs Cb)
= dHo / Ho
or
dTe = (Te / 4) (dHo / Ho)

Recall from the section titled Surface Temperature of an Ideal Rotating Spherical Body that for the whole Earth the effective value of Te is about 278.636 degrees K.

Recall from the section titled Solar Radiation that the variation in Ho is only +/- 3 parts in 1367 with a period of eleven years, corresponding to the sunspot cycle, giving:
dHo / Ho ~ (3 / 1367)

Thus:
dTe ~ (3 / 1367) (278.636 degrees K / 4)
= .153 degrees K

Thus natural variation in Ho associated with the eleven year sunspot cycle causes an average temperature fluctuation of about +/- 0.15 degrees C. Over the 29 year measurement period (1978 to 2007 inclusive) there was no detectable trend for the average value of Ho to either increase or decrease. Hence for the purpose of 40 year global warming trend calculations:
dTe = 0
 

CHANGE IN Ta DUE TO NON-AQUEOUS GREENHOUSE GASES:
For the Earth the emission temperature Ta is the temperature at the dense cloud altitude where most atmospheric water vapor condensation occurs. The emission temperature Ta can be expressed in terms of the theoretical emission temperature Te, the solar albedo Fr, and the infrared emissivity Ft.

The planetary emissivity Ft is calculated from measurements of Ftw(W) made by spacecraft as detailed in the Emissivity section.

The planetary albedo Fr can be quantified by measurement of the Earth's solar reflectivity. The average planetary albedo is a combination of the albedo of the oceans, the albedo of continents and the albedo of cloud cover. The albedo Fr is affected by ice, liquid water and water vapor but is not significantly affected by other atmospheric gases. Hence, in evaluating the effect of a relatively rapid change in atmospheric carbon dioxide concentration on Ta, Fr can be assumed to be constant. In the long term, as the ocean surface temperature increases the average atmospheric water vapor concentration will increase, causing Ft to decrease and possibly causing Fr to increase.

Consider two measurements of Ta taken at the same location with different values of Ft but with the same value of Fr (eg. atmospheric water vapor concentration is constant).
Taa = Te [(1 - Fra) / Fta]^.25
Tab = Te [(1 - Frb) / Ftb]^.25
For:
Fra = Frb
combining these two equations gives:
Tab / Taa = (Fta / Ftb)^.25
or
(Tab - Taa) = Taa[(Fta / Ftb)^.25 - 1]
which is referred to herein as the Non-aqueous Warming Equation.

This equation gives the warming (Tab - Taa) that results from a change in the concentrations of CO2 and other nonaqueous greenhouse gases in the atmosphere, provided that Fr is constant. This equation quantitatively relates non-aqueous warming (Ta2 - Ta1) to parameters that can be obtained from analysis of the earth's infrared thermal emission spectrum using the measured atmospheric carbon dioxide concentration and laboratory measurements of carbon dioxide infrared absorption. Remember that (Tab - Taa) is the non-aqueous warming at cloud level, not ground level.

The nonaqueous warming equation, together with spacecraft gathered infrared thermal emission data and laboratory measurements of gas infrared absorption data, permits calculation of the local warming due to changes in the atmospheric concentrations of carbon dioxide, methane and nitrous oxide. The remaining local warming is due to a change in average atmospheric water vapor concentration or a change in local albedo.
 

THERMAL EMISSION SPECTRUM:
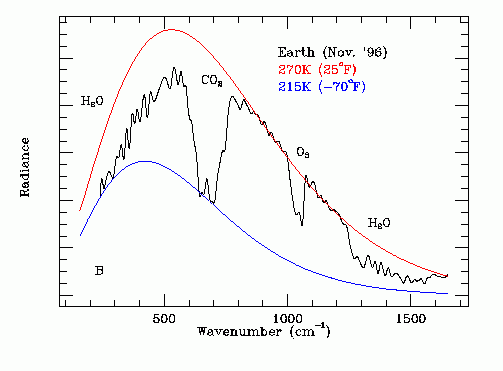
The black line on the following graph gives the experimentally measured thermal emission spectrum of the Earth as recorded by the Mars Global Surveyor space probe on November 23, 1996. Note the H2O, CO2 and O3 absorption bands. Methane (CH4) absorption is in the range 1200 cm^-1 to 1400 cm^-1. Nitrous oxide absorption is co-incident with the CO2 and CH4 absorption bands.

The area under the comparative red 270 K black body thermal emission curve and the area under the black experimentally measured thermal emission data curve were found in the Emissivity section.

Note that at frequencies (or wavenumbers) where the atmosphere is transparent to infrared radiation the red 270 K black body thermal emission curve is tangent to the black experimentally measured thermal emission data curve. Note that at frequencies (or wave numbers) where the atmosphere is opaque to infrared radiation the blue 215 K black body thermal emission curve is tangent to the black experimentally measured thermal emission data curve.

As is obvious from this graph, the largest infrared absorption is by water vapor. Water vapor determines the extent of the baseline greenhouse effect but is not directly responsible for man-made global warming. From a global warming perspective the most important greenhouse gas is carbon dioxide. However, note that CO2 related warming causes an increase in the ocean surface temperature which in turn increases the average atmospheric water vapor concentration and hence reduces Ft, causing further warming.
 

TRANSMITTANCE ANALYSIS:
At any particualr frequency W the infrared transmittance Ftw of the atmosphere os given by: Ftw = 1 / [1 + Coa(W) Pa + Cob(W) Pb + Coc(W) Pc + Cod(WW) Pd + Coe(W) Pe]
where:
Coa(W) = frequency dependent absorbance of the H2O in the atmosphere
Cob(W) = frequency dependent absorbance of the CO2 in the atmosphere
coc(W) = frequency dependent absorbance of the O3 in the atmosphere
Cod(W) = frequency dependent absorbance of the CH4 in the atmosphere
Coe(W) = frequency dependent absorbance of the N2O in the atmosphere
and where:
Pa = partial pressure of H2O;
Pb = partial pressure of CO2;
Pc = partial pressure of O3;
Pd = partial pressure of CH4;
Pe = partial pressure of N2O

Note that outside of their respective absortion bands each of the absorbance Coi(W) functions is zero.

The initial objective is to determine the change in atmospheric emission temperature caused by doubling and tripling of the CO2 partial pressure Pb while holding Pa constant. A second objective is to find the further increases in temperature Ta due to the corresponding increase in atmospheric H2O concentration.

The relative thermal emission within the carbon dioxide absorption band versus
Wavenumber= F / C
is tabulated herein. Note that the thermal emission is low near the center of the carbon dioxide absorption band at:
Wavenumber = 669 cm^-1
and is a local maximum at the edges of the main carbon dioxide absorption band. High resolution satellite data from the period 1969 - 1971 presented in the Infrared Absorption section shows that the CO2 absorption band has a series of significant sidebands. These sidebands cause increasing global warming as the atmospheric CO2 concentration increases.

The change in Ft due to carbon dioxide is found by first determining the thermal emission spectrum that would occur with no carbon dioxide if the atmospheric water vapor concentration remained unchanged. This spectrum determination is done by copying the average relative absorbances at 40 cm^-1 wavenumber intervals from the water vapor absorption data presented in the Infrared Absorption section and then interpolating these values to obtain the relative absorbances at 50 cm^-1 intervals. The results of this interpolation are shown in the table below.

Wavenumber	Average Tabulated    Absorbance	Interpolated Absorbance Coa
450	1961.7	1961.7
490	1721.9
500		1479.8
530	753.6
550		827.1
570	900.6
600		667.0
610	589.2
650	437.0	437.0
690	465.7
700		445.1
730	383.2
750		369.3
770	355.4
800		337.5
810	331.5
850	335.4	335.4

The absorption data at 450 cm^-1, where the direct carbon dioxide infrared absorption is negligible, is scaled using the measured Ftw(W) value and the 270 K black body value at 450 cm^-1 to calculate the Ftw(W) values and the Relative Emission values without carbon dioxide at 50 cm^-1 wavenumber intervals up to 850 cm^-1.

At 450 cm^-1:
(Emission without carbon dioxide)
= (Emission on 270 K BB line) / (1 + (Coa X constant))

Rearranging this equation gives:
1 + (Coa X constant)
= (Emission on 270 K BB Line) / (Emission without CO2)
= 9.25 / 7.3 = 1.26712
or
(Coa X constant) = 0.26712 From above table relative absorbance at 450 cm^-1 is 1961.7. Thus:
constant = 0.26712 / 1961.7 = 1.361676 X 10^-4

For other wavenumbers:
(Emission without carbon dioxide)
= (Emission on 270 K BB line) / (1 + (Coa X constant))
= (Emission on 270 K BB line) / (1 + (Coa X 1.361676 X 10^-4))

This equation is used to calculate the relative emission without carbon dioxide at 50 cm^-1 wavenumber intervals from 500 cm^-1 to 850 cm^-1.

The following table gives the wave number, the relative emission as a function of wavenumber with carbon dioxide copied from the Emissivity section for the carbon dioxide absorption band, and the relative emission without carbon dioxide obtained using the above formula:
 

Wave No. (cm^-1)	Emission With CO2	Emission Without CO2	270 K Black Body Emission
450	7.3	7.303	9.254
500	7.8	7.90927	9.503
550	7.7	8.55904	9.523
600	6.3	8.56967	9.348
650	3.6	8.50963	9.016
700	3.3	8.07273	8.562
750	5.2	7.63696	8.021
800	6.7	7.09972	7.426
850	6.5	6.50396	6.801

 

DATA ANALYSIS:
Recall that at any frequency W where only H2O and CO2 have significant absorption effects:
Ftw = 1 / [1 + Coa Pa + Cob Pb]
or
[1 + Coa Pa + Cob Pb] = (1 / Ftw)
where:
Ftw = (Emission with CO2) / (Black Body Emission)

If there is no CO2 then Ftw becomes Fta where:
Fta = 1 / [1 + Coa Pa]
or
[1 + Co Pa] = (1 / Fta)
where:
Fta = (Emission without CO2) / (Black Body Emission)

Thus:
Cob Pb = [1 + Coa Pa + Cob Pb] - [1 + Co Pa]
= (1 / Ftw) - (1 / Fta)

DOUBLING CO2 CONCENTRATION:
If the concentration of CO2 is doubled Ftw With 2X CO2 becomes:
Ftw2b = 1 / [1 + Coa Pa + 2 Cob Pb]
= 1 / [(1 / Fta) + (2 / Ftw) - (2 / Fta)]
= 1 / [(2 / Ftw) - (1 / Fta)]
= Ftw / [2 - (Ftw / Fta)]

Hence:
(New Emission Data) = Ftw [Black Body Emission] / [2 - (Ftw / Fta)]
= [Emission with CO2] / [ 2 - ([Emission with CO2] / [Emission Without CO2])]
= [Emission with CO2][Emission without CO2] / [2 (Emission without CO2) - (Emission with CO2)]
 

TRIPLING CO2 CONCENTRATION:
If the concentration of CO2 is tripled Ftw With 3X CO2 becomes:
Ftw3b = 1 / [1 + Coa Pa + 3 Cob Pb]
= 1 / [(1 / Fta) + (3 / Ftw) - (3 / Fta)]
= 1 / [(3 / Ftw) - (2 / Fta)]
= Ftw / [3 - (2 Ftw / Fta)]

Hence:
(New Emission Data) = Ftw [Black Body Emission] / [3 - (2 Ftw / Fta)]
= [Emission with CO2] / [ 3 - (2 [Emission with CO2] / [Emission Without CO2])]
= [Emission with CO2][Emission without CO2] / [3 (Emission without CO2) - 2 (Emission with CO2)]
 

Tabulation of these values gives:

Wave No. (cm^-1)	Emission With 2X CO2	Emission With 3X CO2
450	7.297	7.301
500	7.6937	7.990
550	6.9977	8.656
600	4.9808	8.634
650	2.2829	8.578
700	2.0739	8.094
750	3.9421	7.683
800	6.3429	7.132
850	6.4960	6.555

 

These values are plugged into the computer program to calculate the Ft values for 2X CO2 while holding the atmospheric water vapor concentration constant.

Recall that from the web page titled Emissivity the Ft value with an atmospheric CO2 concentration as on November 23, 1996 as measured at Mona Loa of 360.76 ppmv (1X CO2) was:
0.755492

For the same water vapor concentration 2X CO2 yields Ft = 0.7170224.
 

CHANGE IN TEMPERATURE:
Recall that if Fr is constant:
(Tab - Taa) = Taa[(Fta / Ftb)^.25 - 1]
where:
Taa = 270 deg K; Initial CO2 = 360.76 ppmv
Fta = 0.755492

For 2X CO2 = 2 X 360.76 ppmv = 721.52 ppmv:
Ftb = 0.7170224

(Tab - Taa) = Taa[(Fta / Ftb)^.25 - 1]
= 270 K [(0.755492 / 0.7170224)^0.25 - 1]
= 3.15 deg K

Sudden doubling the atmospheric CO2 concentration from its November 1996 value of 360.76 ppmv to a future new value of 2(360.76 ppmv) = 721.52 ppmv causes a step increase in the atmospheric emission temperature of 3.15 degrees C. This atmospheric temperature increase enables an increase in the atmospheric water vapor pressure and hence a corresponding increase in the atmospheric water vapor concentration. In the temperature region 263 K to 278 K a 10 degree K temperature increase causes the atmospheric water vapor pressure to approximately double.

Temperature (deg C)	H2O Vapor pressure in mm Hg
-10	2.15
0	4.58
+1	4.9
+2	5.3
+3	5.7
+4	6.1
+5	6.5

 

CHANGE IN EMISSIVITY DUE TO SUDDEN DOUBLING OF THE ATMOSPHERIC H2O CONCENTRATION:
Similarly the change in emissivity due to a sudden doubling of the atmospheric water vapor concentration can be evaluated provided that Fr remains constant.

Wavenumber (cm^-1)	El=215 K Black Body	Measured Eb	Eh = 270 K Black Body	(Eb - Ec)
0	0	0	0	0
50	0.6E	0.4E	0.416	0
100	1.2E	1.2E	1.443	0
150	2.0	2.0E	2.800	0
200	3.0	3.0E	4.269	0
250	3.65	4.1	5.689	.346
300	4.3	4.9	6.949	.471
350	4.65	5.9	7.980	.769
400	4.8	6.3	8.751	.938
450	4.8	7.3	9.254	1.096
500	4.55	7.8	9.503	1.045
550	4.3	7.7	9.523	0 - CO2
600	3.95	6.3	9.348	0 - CO2
650	3.6	3.6	9.016	0 - CO2
700	3.3	3.3	8.562	0 - CO2
750	2.85	5.2	8.021	0 - CO2
800	2.4	6.7	7.426	.282
850	2.1	6.5	6.801	.281
900	1.75	6.16	6.169	0
950	1.5	5.54	5.547	0
1000	1.25	4.94	4.949	0
1050	1.05	3.0	4.384	0 - O3
1100	0.85	3.85	3.859	0
1150	0.7	3.37	3.376	0
1200	0.55	2.93	2.936	0
1250	0.40	2.3	2.542	.221
1300	0.3	1.0	2.190	.435
1350	0.25	1.0	1.878	.398
1400	0.25	0.9	1.605	.337
1450	0.2	0.7	1.366	.283
1500	0.1	0.5	1.158	.248
1550	0.1	0.6	0.979	.222
1600	0.05	0.7	0.825	.087
1650	0.05	0.69	0.693	0
1700		0.6E	0.581
Column Total:				7.459

INCREASE IN TEMPERATURE DUE TO SUBSEQUENT DOUBLING OF THE ATMOSPHERIC H2O CONCENTRATION WHILE Fr = CONSTANT:
(-dFt / Ft) = 7.459 / (123.1 - 3.751) = 7.459 / 119.249 = .0625
Ta = 270 + 2.058 = 272.058
giving:
dTa = (272.258 / 4)(.0625) = 4.254 degrees C

ITTERATIVE PROCESS:

1st Itteration:
From a steam table, a 2.058 degree C = 3.7044 degrees F open water surface temperature increase causes a H2O vapor pressure increase of:
(3.7044/3) X (.27494 psia - .24713 psia) = .0343397 psia
At 59 F the absolute pressure was .24713 psia, so the fractional increase in H2O vapor pressure was: .0343397 / .24713 = .13895
The corresponding increase in atmospheric temperature caused by this increased H2O vapor pressure is:
.13895 X 4.254 degrees C = .5911 degrees C
Hence the new value of the atmospheric temperature increase is:
2.058 C + .5911 C = 2.6491 C

2nd Itteration:
From a steam table, a 2.6491 C = 4.768 F open water surface temperature increase causes a H2O vapor pressure increase of:
(4.768 / 4) X (.28480 psia - .24713 psia) = .04490 psia
At 59 F the absolute H2O vapor pressure was .24713 psia, so the fractional increase in H2O vapor pressure was:
(.04490 / .24713) = .18169
The corresponding increase in atmospheric temperature caused by this increased H2O vapor pressure is:
.18169 X 4.254 = .7729 C
Hence the new value of the atmospheric temperature increase is:
2.058 + .7729 = 2.8309 C

3rd Itteration:
From a steam table a 2.8309 C = 5.0957 F open water surface temperature increase causes a H2O vapor pressure increase of:
(5.0957 / 5) X (.29497 psia - .24713 psia) = .04876 psia
At 59 F the absolute H2O vapor pressure was .24713 psia, so the fractional increase in H2O vapor pressure was:
(.04876 / .24713) = .19728
The corresponding increase in atmospheric temperature caused by this increase in H2O vapor pressure was>
.19728 X 4.254 = .8392 C
Hence the new value of the atmospheric temperature increase is:
2.058 C + .8392 C = 2.8972 C

4th Itteration:
From a steam table a 2.8972 C = 5.215 F open water surface temperature increase causes a H2O vapor pressure increase of:
(5.215 / 5) X (.29497 psia - .24713 psia) = .04990 psia
At 59 F the absolute H2O vapor pressure was .24713 psia, so the fractional increase in H2O vapor pressure was:
(.04990 / .24713) = .2019
The corresponding increase in atmospheric temperature caused by this increase in H2O vapor pressure was>
.2019 X 4.254 = .8589 C
Hence the new value of the atmospheric temperature increase is:
2.058 C + .8589 C = 2.917 C

5th Itteration:
From a steam table a 2.917 C = 5.2504 F open water surface temperature increase causes a H2O vapor pressure increase of:
(5.2504 / 5) X (.29497 psia - .24713 psia) = .0502358 psia
At 59 F the absolute H2O vapor pressure was .24713 psia, so the fractional increase in H2O vapor pressure was:
(.0502358 / .24713) = .2033
The corresponding increase in atmospheric temperature caused by this increase in H2O vapor pressure was>
.2033 X 4.254 = .8647 C
Hence the new value of the average atmospheric temperature increase is:
2.058 C + .865 C = 2.923 C

SUMMARY:
Doubling the atmospheric CO2 concentration from its November 1996 value of 360.76 ppmv to a future value of 721.52 ppmv causes a direct average emission temperature increase of 3.15 C and if the planetary albedo Fr = constant causes a further average emission temperature increase of 0.865 C due to an increased atmospheric water vapor concentration for a total average emission temperature increase of:
3.15 C + 0.865 C = 4.015 deg C .

The reader is reminded that 3.15 C is the emission temperature increase that will occur when the atmospheric CO2 concentration as measured at Mauna Loa, Hawaii is doubled but the atmospheric water vapor concentration is held constant.

The corresponding ground level temperature increase in urban areas is substantially larger due to the proximity of local sources of heat, CO2, and H2O vapor (electric power dissipation, nuclear reactors, cooling towers, combustion of coal, combustion of hydrocarbon fuels) and due to the extensive use of black asphalt (which affects local albedo) for both road surfaces and building roofs. This extra temperature increase is sometimes known as the urban heating effect.

The corresponding temperature increase in polar areas is also substantially larger due to a change in local albedo caused by melting of ice and snow.

Hence, total warming is a combination of global warming and local warming effects.

IN NOVEMBER 1996:
Tb = 270 K
Ft = Ftb
= .755492
from the EMISSIVITY web page;
(CO2) = 360.76 ppmv from Carbon dioxide concentration measurements at Mauna Loa for November 1996

Note that there is about a 4% discrepency between the November 1996 value of:
Ft = 0.755492
calculated above by integration over the thermal emission spectrometer output and the November 1996 value of:
Ft = 0.7973495
calculated from measurements of the average emission temperature and the planetary albedo as set out on the web page titled THERMAL RUNAWAY. At this time this author is uncertain as to the cause of this discrepency. This author suspects that this discrepency is due to partial thermal emission spectrometer response at the high and/or low frequency ends of its range. However, it is possible that there is zero reference problem with the thermal emission spectrometer or that there is systematic error in the planetary albedo measurement.
 

CALCULATION OF A FUTURE Ft VALUE:
Let Ftc be the value of Ft at an atmospheric CO2 concentration of 721.52 ppmv, twice the November 1996 value of 360.76 ppmv.
As calculated above:
Ftb = 0.755492
Ftc = 0.7170224

Hence:
(Ftb - Ftc) / Ftb
= [1 - (.717024 / .755492)] = .0509178
This value is of importance in quantifying the additional irrigation required to maintain the same crop temperature versus time profile before and after doubling of the atmospheric CO2 concentration.

GLOSSARY OF TERMS

This web page last updated November 2, 2015.